Goal: When you have finished this laboratory exercise you will understand
- about different mathematical models used in predictive microbiology to evaluate microbial growth
and you will learn
- how to determine the parameters required for the Gompertz model using experimentally obtained microbial growth data, and
- how to compare the predicted and experimental results to examine the suitability of the model.
-
Predictive microbiology deals with developing accurate mathematical models to describe the microbial proliferation in food products as a function of environmental conditions to control the risk for food safety.
The models use experimental data and equations for prediction, and microbial safety can be estimated without applying traditional microbiological enumeration techniques. When an appropriate model is developed and experimentally validated, it enables prediction of the effect of different variables (e.g., temperature, pH) on microbial evolution.
Therefore combining predictive microbiology models with food processing is an effective method to manage food safety.
-
We have selected Escherichia coli for this experiment since some of its serotypes (especially O157:H7) can cause serious food poisoning.
Experiments will be accomplished at three different temperatures (27, 30 and 36 oC).
The initial samples of the cell suspensions in the nutrient broth for enumeration will be taken immediately after the come-up time (t = 0), and the enumeration will be conducted at different time steps.
The initial cell concentration is 10-4 cfu/ml, where cfu is colony forming units.
-
The microbial spoilage of food products and the survival of pathogens through the pasteurization/sterilization processes are of major importance to the food process industries because they directly affect the consumer's health and safety.
Traditionally, the microbiological safety of food products has been established via microbial tests.
Predictive modeling is a promising field of food microbiology where mathematical models are used to describe the behavior of the microorganisms under different conditions (e.g. T, pH, aw). A number of mathematical models and equations have been developed to express microbial growth in food products and culture media.
Among these models, Gompertz equation and its modified form has been successfully applied to describe the growth of different pathogen microorganisms: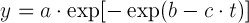
where, t is time, and a, b and c are the Gompertz equation parameters that may describe the 3-phases of a growth curve (lag phase, logarithmic or exponential phase and stationary phase).
-
In this laboratory exercise, we will conduct an experiment involving the enumeration of an Escherichia coli suspension subjected to constant temperature changes and determine the Gompertz equation parameters from bacterial growth results.
Mathematical and graphical approaches will be presented for this purpose.
-
In this laboratory exercise, you obtained experimental data on the Escherichia coli growth at a given constant temperature. Data analysis will involve determining the modified Gompertz equation parameters.
To determine the modified Gompertz equation parameters: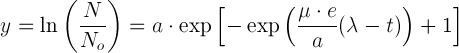
1. Copy an experimentally obtained data in a new Excel file. The experimental data is N versus incubation time (t, hrs),
2. In a new column, determine the ln(N/No), and create a scatter plot versus time: -
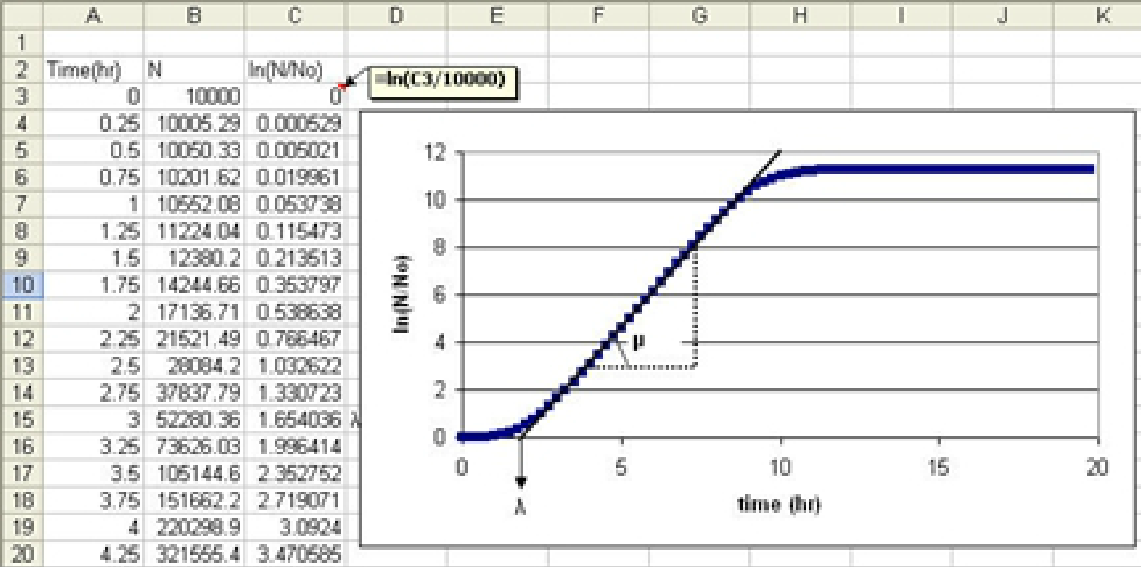
3. Find the inflection of the plot and determine the lag time and the tangent line by using data for the linear part visually as shown in the above figure,
4. Then, create a second plot to determine the tangent in the inflection point and the lag time applying the Trendline feature of Excel. -

5. Then, determine the required parameters of the Gompertz equation using the results of Step 4 and the given equations.
6. Based on the given trendline, the specific growth rate becomes 1.4773 while the lag time is 2.7549/1.4773 = 1.8648. -
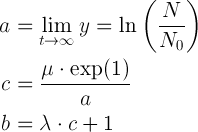
where, μ is the specific growth rate, and λ is the lag time.
-
7. Using the determined equation parameters, obtain the ln(N/N0) versus time and compare the results with the experimental data.
8. Repeat this procedure for the other sets of the experimental data.
Discuss how well your model fits the experimental data. Is there any lack of it? If that is the case, which part of the growth curve is that lack more obvious? How would you minimize the lack of data fit?
How did the modified Gompertz equation parameters change with respect to temperature? Is there any trend?
Conduct a literature search on this subject and suggest any improved model to better fit the experimental data.
- Baranyi, J. and Roberts, T.A. (1995). Mathematical of predictive food microbiology. Int. J. Food Microbiology. 26: 199-218.
- Fujikawa, H., Kai, A., and Morozumi, S. (2004). A new logistic model for Escherichia coli growth at constant and dynamic temperatures. Food Microbiology. 21: 501-509.
- Gil, M.M., Brandao, T.R.S., and Silva, C.L.M. (2006). A modified Gompertz model to predict microbial inactivation under time-varying temperature conditions. J. Food Eng. 76:89-94.