Goal: When you have finished this laboratory exercise you will understand
- how liquid foods are heated in a steam-jacketed kettle
and you will learn
- how to determine the rate of heating of a liquid food in a well-mixed steam-jacketed kettle
- the effect of kettle surface temperature and convective heat transfer coefficient on the rate of heat transfer
-
Liquid foods are often heated in steam-jacketed kettles. These kettles are typically made of stainless steel, and as the name suggests, a steam jacket surrounds the kettle. Typically, a mixer in the kettle is used to keep the liquid food well mixed during heat. This prevents any temperature gradient to develop within the liquid food. At any instance of time, the temperature anywhere in the kettle is the same. Some examples of steam-jacketed kettles are as follows:
- Hemispherical steam jacketed kettles
- Steam jacketed kettles with mixer or paddles
- Steam jacketed kettles with wiping blades.
-

A kettle with a mixer
Courtesy: Lee Industries. -
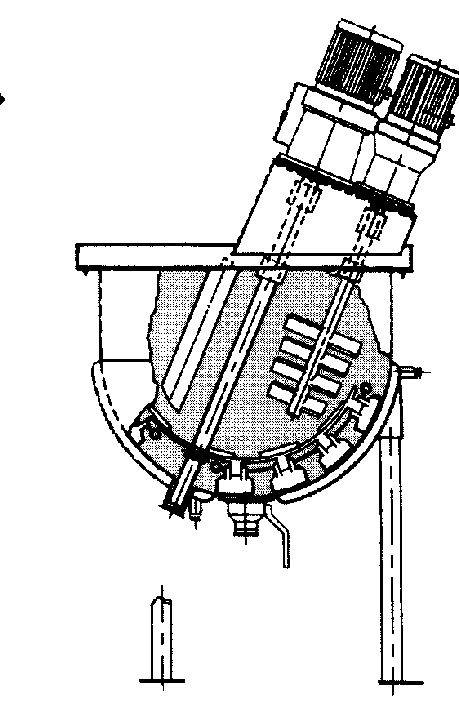
A kettle with a mixer
Courtesy: Lee Industries.
-
In a laboratory experiment, we use a steam jacketed kettle to heat tomato juice. The following steps are used:
1) Fill the kettle partially with tomato juice.
-
2) Start the mixing paddle and open the steam inlet valve into the kettle.

-
3) Adjust the steam pressure to obtain a desired inside surface temperature of the kettle. Measure the juice temperature by locating a thermocouple probe in the juice, making sure that it does not entangle with the paddle.

-
4) Record the juice temperature with a data acquisition system.
-
In the virtual experiment, enter the initial temperature of juice, the kettle-surface temperature, radius of the kettle, the convective heat transfer coefficient, and the heating time. The paddle speed is indirectly reflected by the magnitude of the inside convective heat transfer coefficient. You will obtain the temperature history of the juice during heating.
-
When the temperature of an object changes with time, we have transient (or unsteady state) heat transfer. In case of solid foods, during transient heat transfer, temperature changes with time and location, and the mathematical treatment of such a case is complicated. However, when liquid foods are heated and well mixed, then the temperature of the liquid changes only with time. For this case, the Biot number is less than 0.1 and we can use lumped system analysis.
-
The temperature of the juice is described by expressing the temperature ratio as an exponential relationship with time, as follows:
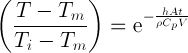
Where T is unknown temperature, Tm is the temperature of heating surface, Ti is the initial temperature, h is the convective heat transfer coefficient, A is the contact area, ρ is the density of tomato juice, Cp is the specific heat of the tomato juice, V is the volume, and the t is the variable time.
-
The lumped capacity analysis is unsteady state heat transfer is based on the fact that at any instance of time, the temperature at any location inside an object is the same. In our case, if the juice in the kettle is well mixed then the temperature at any time will be the same anywhere in the kettle. Note that this criterion is true for a liquid food only if it is well mixed. The temperature-time data collected in this experiment for different operating conditions should be plotted as XY scatter plots. Observe the relationship of temperature vs. time.
-
The rate of heating may be obtained by using the following steps:
1) Create a column of ln[(T - Tm/(Ti - Tm)] vs. time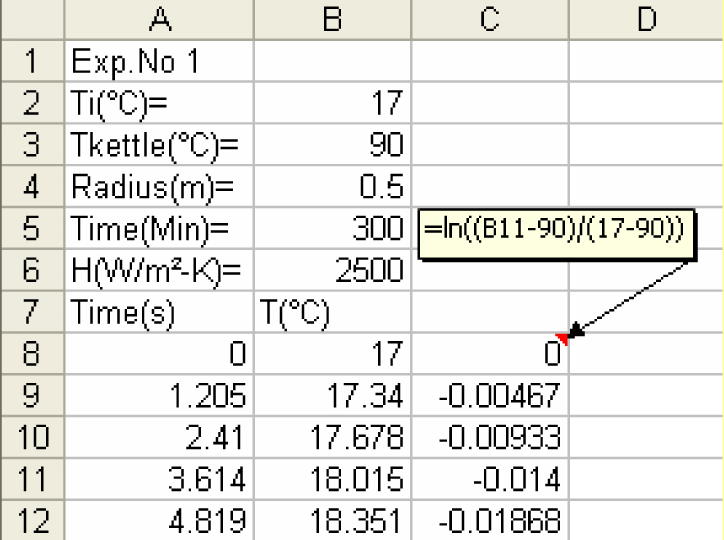
-
2) Create a scatter plot of natural logarithm of temperature ratio vs. time. Using Trend line determine the equation of the straight line.
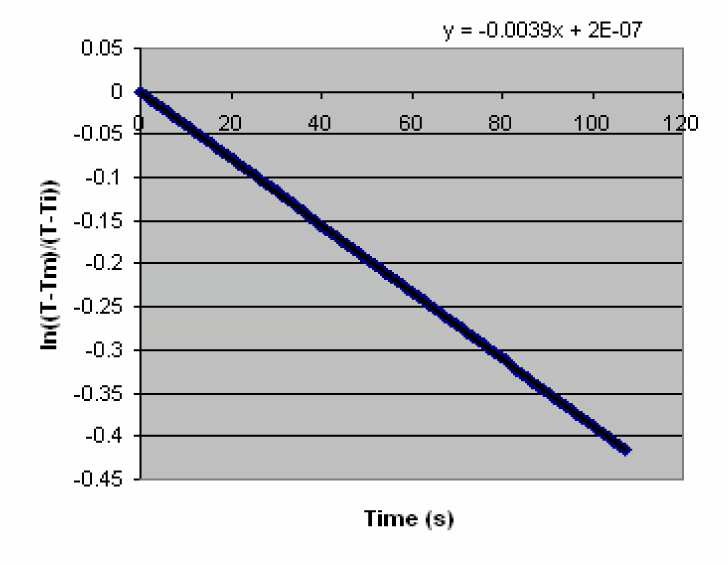
-
3) The slope of the straight line through the linear portion of the plot gives the rate of heating with units of 1/time.

- Does juice temperature increase with increasing convective heat transfer coefficient at any constant kettle surface temperature? Why?
- What is the role of the kettle surface temperature and convective heat transfer coefficient on the heating process?
- Why is the assumption of lumped capacity valid for heating juice in a kettle?
- Lewis, M.J.(1987). Physical Properties of Foods and Food Processing Systems. Ellis Horwood Ltd. Chichester.
- Singh, R.P. and Heldman, D.R. (2009). "Introduction to Food Engineering," 4th ed., Academic Press, London.