Goal: When you have finished this laboratory exercise you will understand
- the role of convective heat transfer coefficient in heating and cooling applications
and you will learn
- how to measure convective heat transfer coefficient in still air, moving air, and hot water.
- the use of lumped capacity method to determine convective heat transfer coefficient from temperature-time data.
- the influence of product size, air and water temperature, and air and water velocity on the magnitude of convective heat transfer coefficient.
-
Knowledge of heat transfer coefficient, h, is often required in designing and analyzing food processing equipment. Two common approaches are used in the industry to determine h.
The first involves using a heat flux sensor, and the second requires heating or cooling a physical object that simulates a food product undergoing processing
-
We will use the second approach. The physical object, also called a transducer, is made of a high thermal conductivity material, such as copper or aluminum, and it resembles the shape and size of the food product.
For Example, a transducer of an orange will be a solid copper or aluminum sphere of the same diameter as the orange. The internal temperature history of the transducer is measured when exposed to the same conditions as the food product.
Transducer of an orange made of aluminum
-
In a laboratory experiment we use aluminum spheres of different radii as transducers. Each aluminum sphere has a thermocouple embedded at the geometric center. This requires first drilling a hole in the sphere, of about the same diameter as the thermocouple, then inserting the thermocouple into the sphere, so that the measuring junction of the thermocouple is located at the geometric center of the sphere. The procedural steps are as follows:
-
Heat transfer coefficient in an air blast:
1) Heat water in the hot water bath to 95oC.
-
2) Determine the diameter of the aluminum ball using a caliper.

-
3) Connect the thermocouple leads of one of the aluminum spheres to a data acquisition system.

-
4) Place the aluminum ball in hot water bath. when the sphere temperature reaches 95oC, remove it from the bath and place it in the environment where h-value is to be determined.

-
5) To determine h-value in forced air, start the fan, with the air directed to the hanging sphere. Begin recording temperature. When sphere temperature cools down to about 30oC, stop recording the temperature.

-
6) Repeat the previous steps with the other two spheres.
Repeat the entire experiment to determine h-value in stagnant air and hot water.
-
In a virtual experiment, select the diameter of the sphere. From the operator's panel, select initial temperature, fluid temperature and air velocity. Determine temperature vs. time data as the sphere cools from the initial temperature.
-
A thermal energy balance around a solid metal object gives
Energy in = Energy out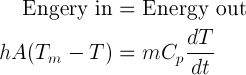
where h is the convective heat transfer coefficient, A is the surface area, Cp is the specific heat of the object, Tm is the surrounding fluid temperature, T is the temperature of the object, t is the time.
.The above equation may be integrated to give
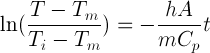
-
The last equation shown in the preceding slide is that of a straight line when ln(temperature ratio) is plotted vs. time. The slope of the linear plot is used to determine the heat transfer coefficient.
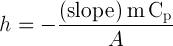
Operator's Panel
Virtual Experiment
-
The results saved in this excercise include sets of temperature-time data for heating/cooling of aluminum spheres in air and water. Use the following steps to analyze the results to determine h-values.
1) For each set of temperature-time data, prepare a new column containing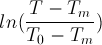
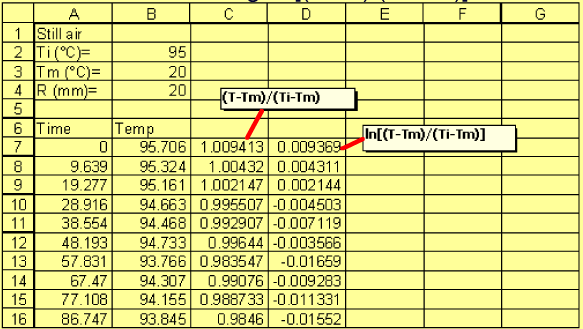
-
2) Create a scatter plot of
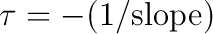 vs. time. Using Trend Line, determine slope of the linear portion of the plot.
vs. time. Using Trend Line, determine slope of the linear portion of the plot.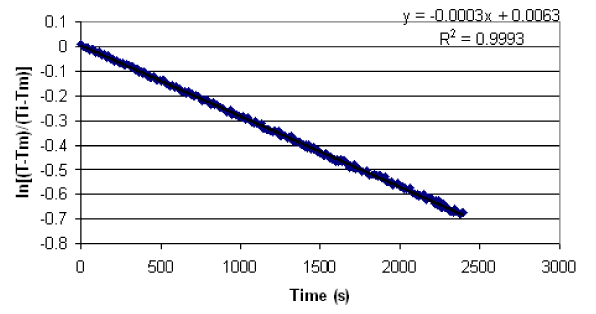
-
3) Calculate the h-value from the following equation using slope, specific heat of aluminum, and mass and surface area of the aluminum sphere.
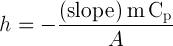
- Discuss how the transducer (sphere) size influence the convective heat transfer coefficient.
- Discuss the effect of air velocity on the convective heat transfer coefficient.
- List any limitations in the experimental procedures that may be sources of error?
- Cengel, Y.A. (1998). "Heat Transfer: A Practical Approach.," McGraw Hill, Inc. Highstown.
- Erdogdu, F., Balaban, M.O., and Chau, K.V. (1998). Automation of heat transfer coefficient determination: Development of a Windows-based software toolo. Food Technology in Turkey. 10:66-75.
- Geankoplis, C.J.(1993). "Transport Processes and Unit Operations," Prentice Hall, Inc. Englewood Cliffs.
- Nicolai, B.M. and Baerdemaeker, J.D. (1996). Sensitivity analysis with respect to the surface heat transfer coefficient as applied to thermal process calculations. Journal of Food Engineering. 28:21-33.